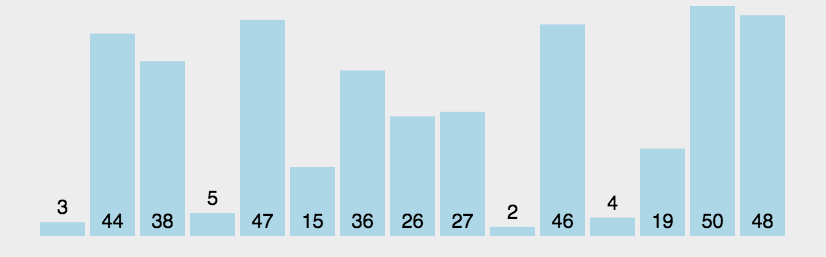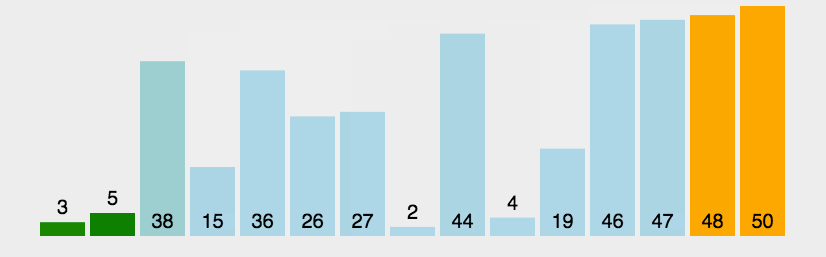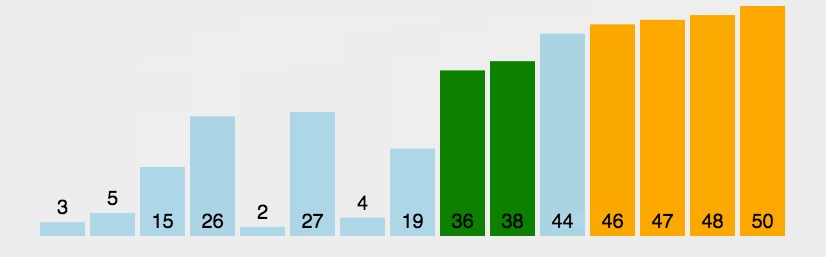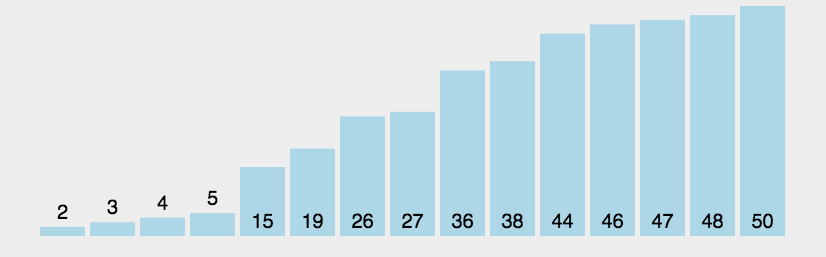reference:
This is my study note of algorithm.
排序算法
1、插入排序
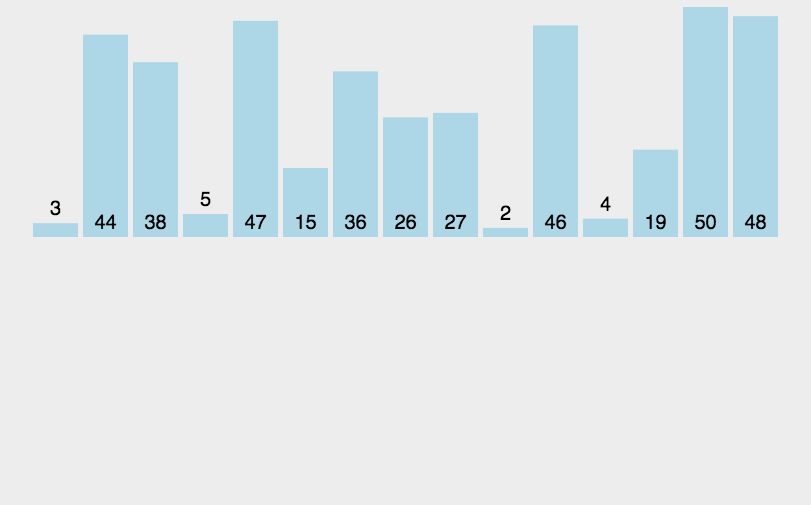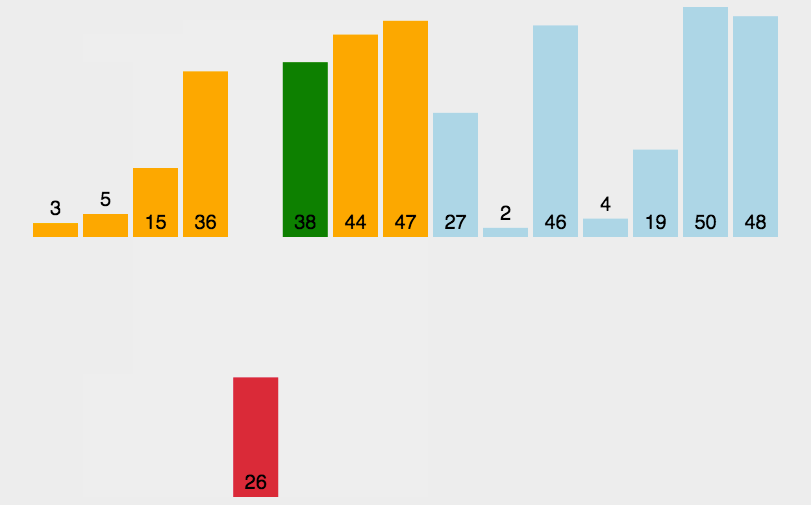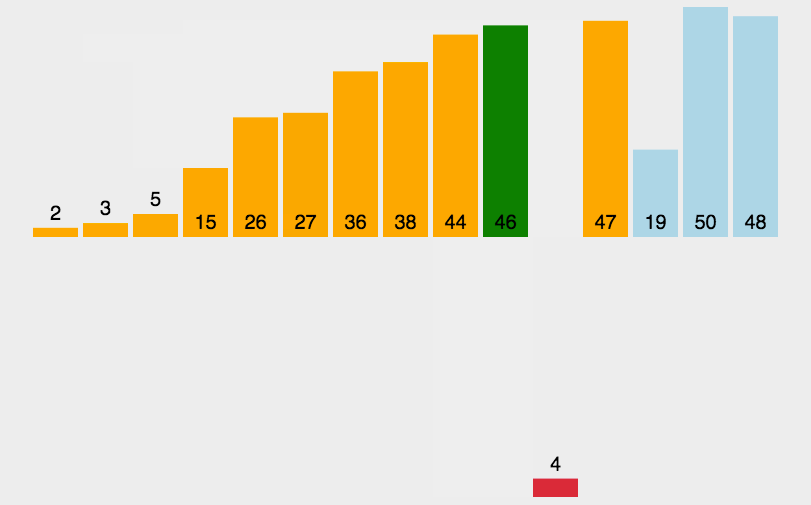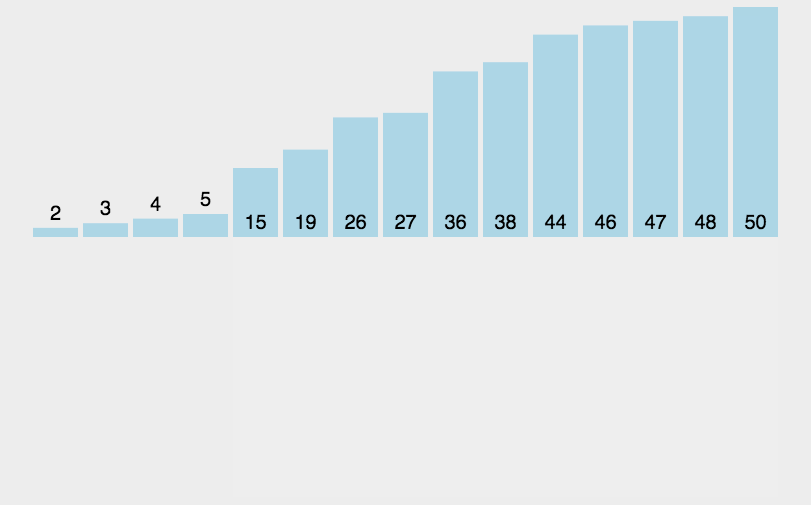
从上图中我们可以得到:
- 首先认为第一个数据已排序
- 从第item数据开始,从后往前排序,直到无法再前进
- 遍历到无法前进时,插入到此时的位置
- 重复上述操作,直到排序完全
| 情况 |
时间复杂度度 |
空间复杂度 |
| 最差 |
$O(N^2)$ |
O(1) |
| 最优 |
$O(N)$ |
O(1) |
代码表示如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| void inSert(int *data, int num)
{
for(int i=0; i < num-1; i++)
{
int end = i;
int item = data[end+1];
while(end>=0)
{
if(item < data[end])
{
data[end+1] = data[end];
end--;
}else
{
break;
}
}
data[end+1] = item;
}
}
|
2、希尔排序
先选定一个小于N的整数gap,此时我们将间距相距gap的数据与剩余数据进行分组,对于各分组中的数据进行插入排序。由于对数据进行预排列,数据的步长减少,因此复杂度相比于插入排序好。
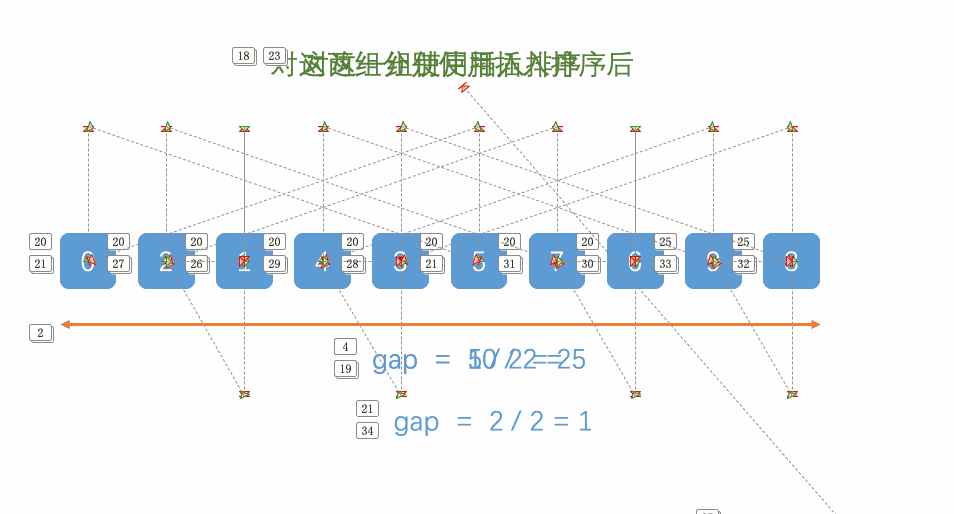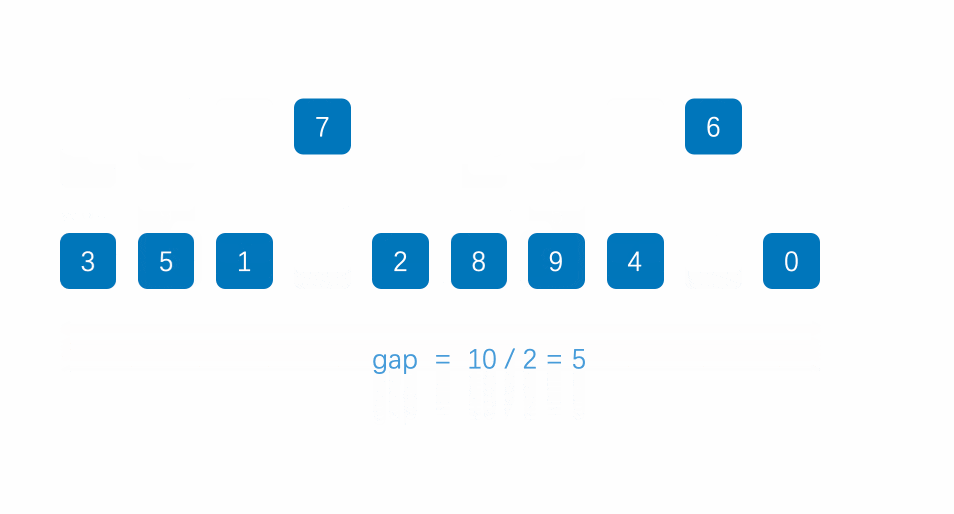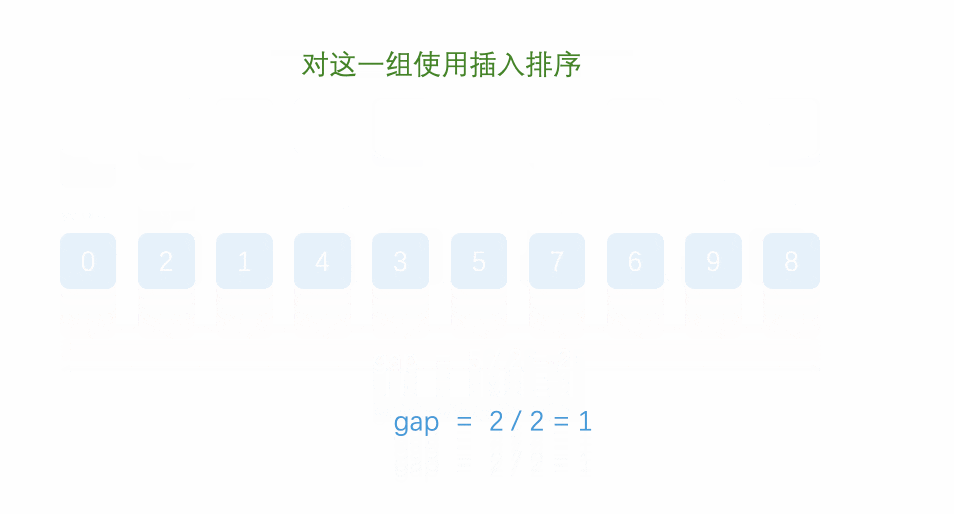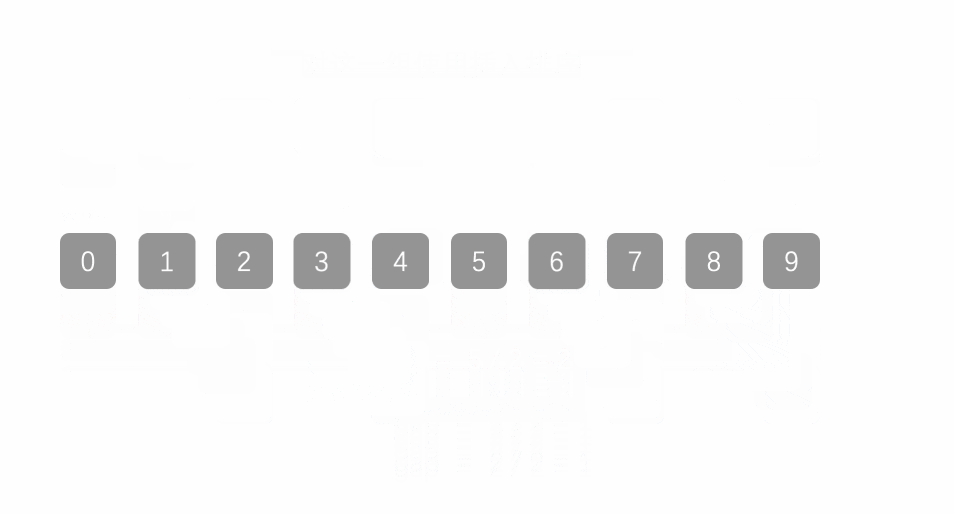
从上图中我们可以得到:
- 首先根据间距gap进行分组
- 对各组数据进行插入排序
- 重复上述操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| void shellSort(int *data, int n)
{
int gap = n;
while(gap>1)
{
gap = gap / 2;
for(int i=0; i < n - gap; i++)
{
int end = i;
int item = data[end+gap];
while(end>=0)
{
if(item < data[end])
{
data[end+gap] = data[end];
end = end-gap;
}else
{
break;
}
}
data[end+gap] = item;
}
}
}
|
| 情况 |
时间复杂度度 |
空间复杂度 |
| 平均 |
$O(N^{1.3})$ |
O(1) |
3、选择排序
先看图:
选择排序以开头数据为起始,往后遍历寻找满足条件的值,随后将数据进行交换。下述代码中采用双向选择,即一边寻找最大,一边寻找最小,加快了程序的运行速度。
具体操作:
- 向左向右遍历寻找最大最小值所在标签
- 对应标签数据交换
- 重复上述过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| void swap(int *a, int *b)
{
int c = *a;
*a = *b;
*b = c;
}
void selsect(int *data, int num)
{
int begin = 0;
int end = num-1;
while(begin<end)
{
int min = begin;
int max = begin;
for(int i=begin; i <= end; i++)
{
if(data[min] > data[i])
{
min = i;
}
if(data[max] < data[i])
{
max = i;
}
}
if(begin == max)
{
max = min;
}
swap(data[begin], data[min]);
swap(data[end], data[max]);
begin++;
end--;
}
}
|
| 情况 |
时间复杂度度 |
空间复杂度 |
| 最差 |
$O(N^2)$ |
O(1) |
| 最优 |
$O(N^2)$ |
O(1) |
冒泡排序
同样看图:
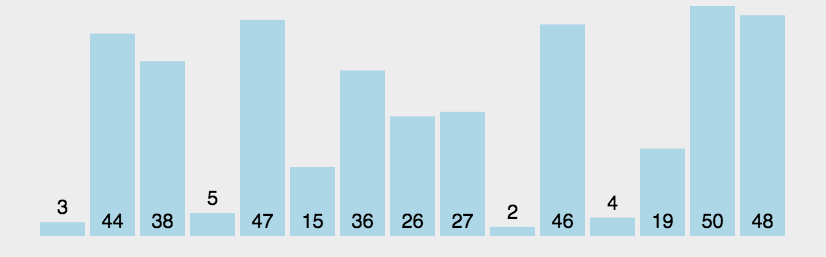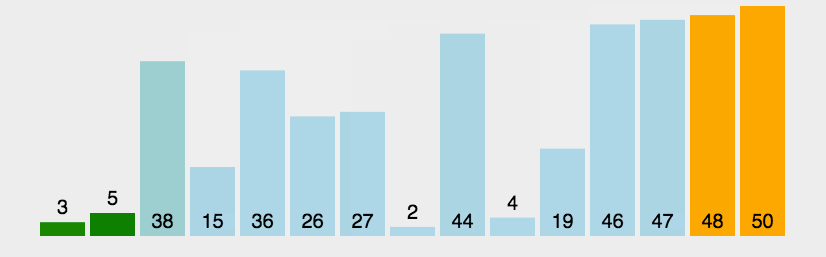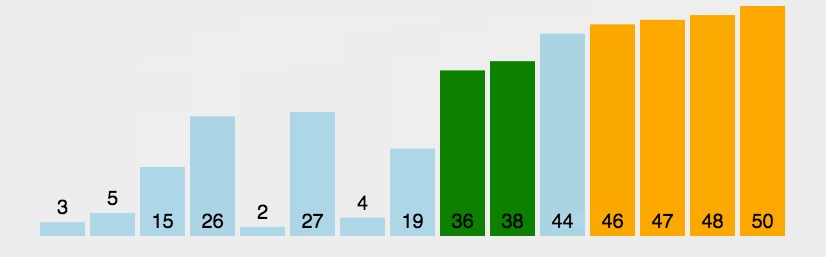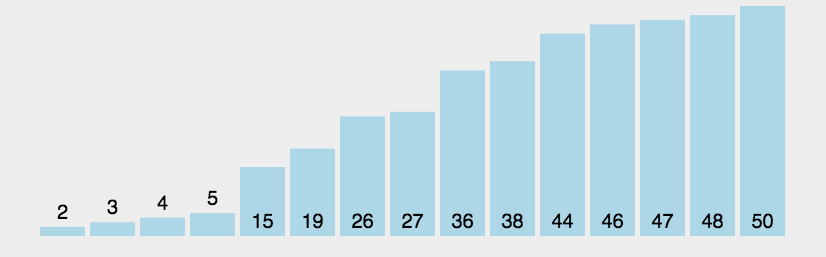
左边大于右边时,交换数据,将最大值换至最右边,以此类推。
具体操作:
- 对比左右两个元素,若右边大,则数据不交换,若左边大,则数据发生交换
- 重复执行上述操作,当排序结束或者遍历结束后退出循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| void bubSort(int *data, int num)
{
int end = num;
int flag = 0;
while(end--)
{
flag = 0;
for(int i=0;i<num;i++)
{
if(data[i]>data[i+1])
{
int n = data[i];
data[i] = data[i+1];
data[i+1] = n;
flag = 1;
}
}
if(flag == 0)
{
break;
}
}
}
|
| 情况 |
时间复杂度度 |
空间复杂度 |
| 最差 |
$O(N^2)$ |
O(1) |
| 最优 |
$O(N)$ |
O(1) |
堆排序
堆排序分为两个部分,处理大顶堆以及堆排序。
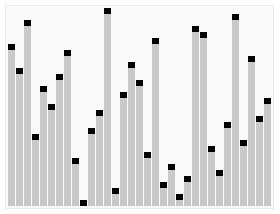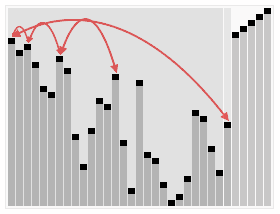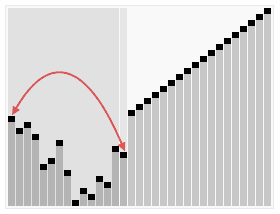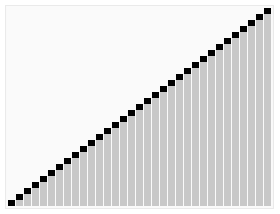
这里要记住:
- 任意节点i的父节点为 2/i-1
- 左子节点 2*i+1
- 右子节点 2*i+2
具体操作:
- 对各个节点进行大顶堆配置
- 排序
- 对节点进行大顶堆配置
- 排序
- 重复上述操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| void maxHeap(int data[], int n, int i)
{
int largest = i;
int ldata = 2*i+1;
int rdata = 2*i+2;
if(ldata<n && data[largest]<data[ldata])
{
largest = ldata;
}
if(rdata<n && data[largest]<data[rdata])
{
largest = rdata;
}
if(largest != i)
{
mySwap(&data[largest], &data[i]);
maxHeap(data, n, largest);
}
}
void heap_sort(int *data, int n)
{
for(int i = n/2-1; i>=0; i--)
{
maxHeap(data, n, i);
}
for(int i = n-1; i > 0; i--)
{
mySwap(&data[0], &data[i]);
maxHeap(data, i, 0);
}
}
|
| 情况 |
时间复杂度度 |
空间复杂度 |
| 最差 |
$O(nlogn)$ |
O(1) |
| 最优 |
$O(nlogn)$ |
O(1) |
快排
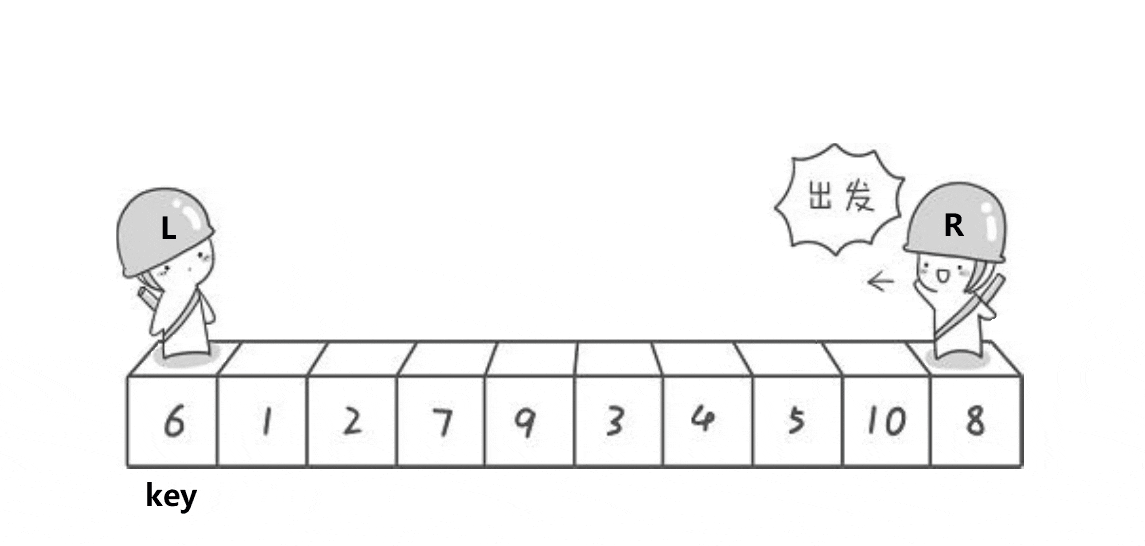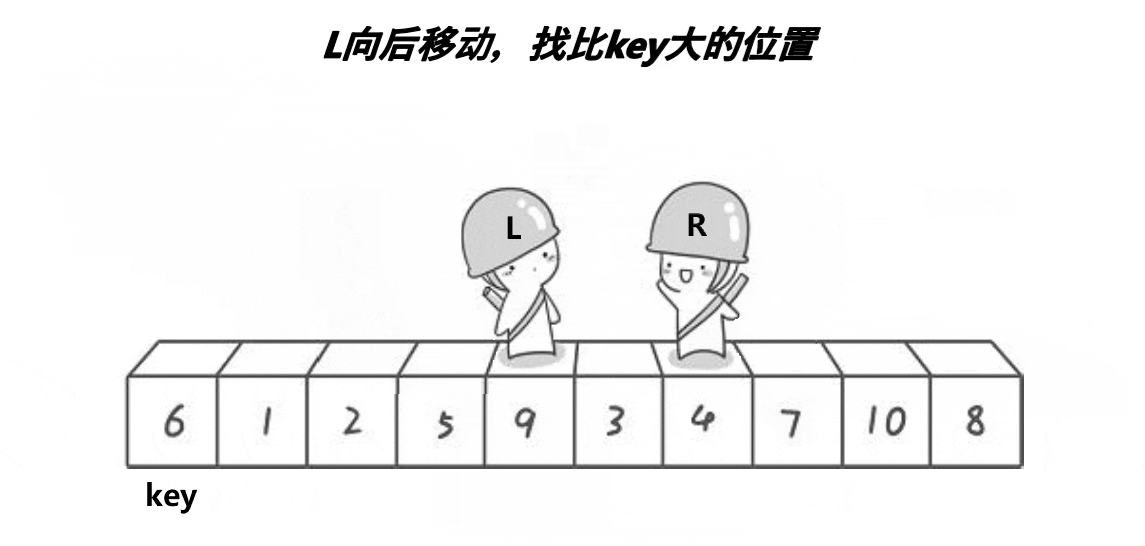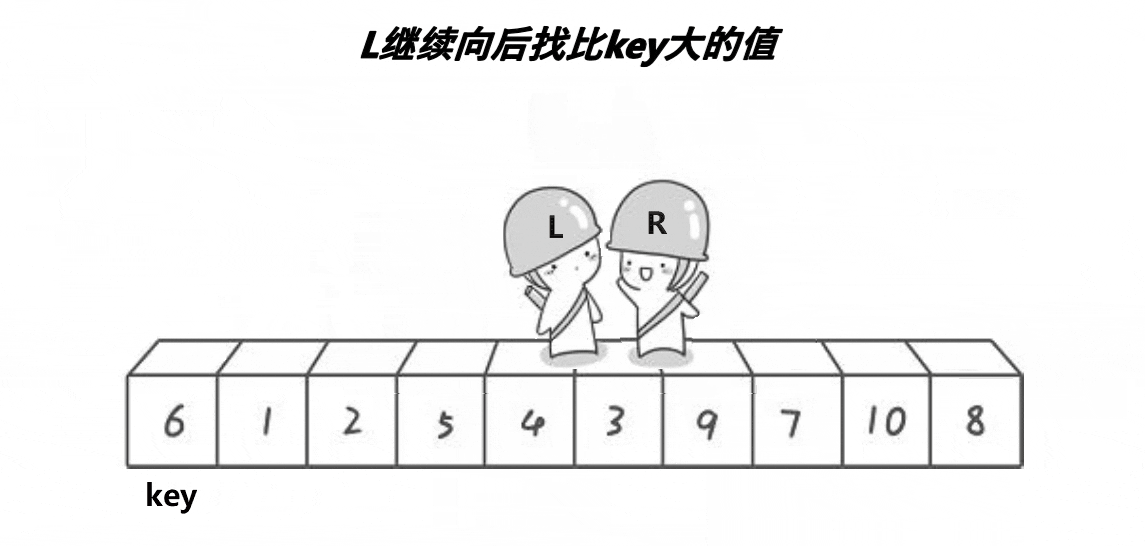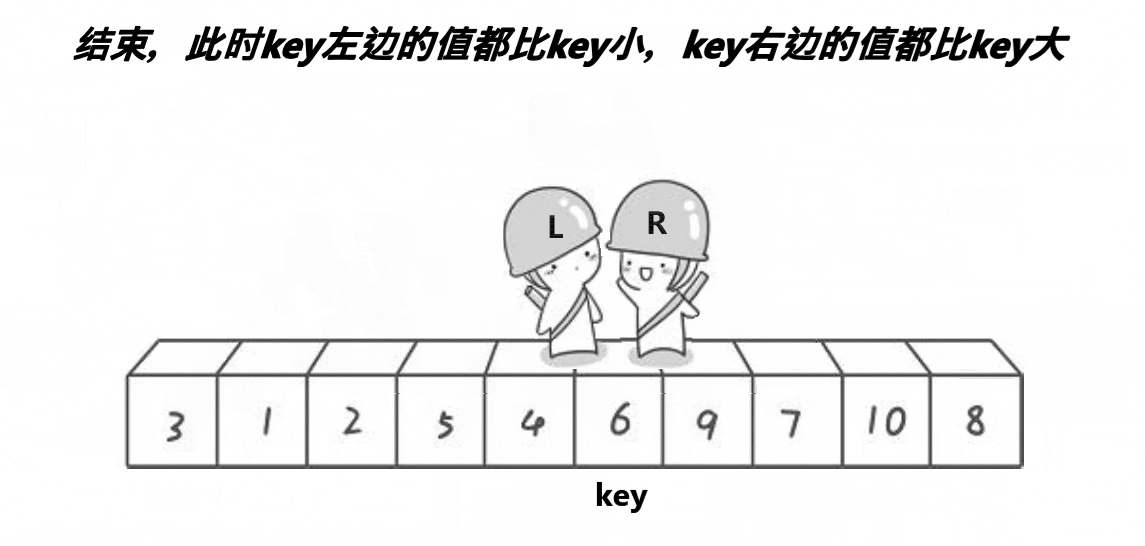
- 选出一个key,一般是最左边或是最右边的
- 定义一个begin和一个end,begin从左向右走,end从右向左走
- 在走的过程中,若end遇到小于key的数,则停下,begin开始走,直到begin遇到一个大于key的数时,将begin和right的内容交换,end再次开始走,如此进行下去,直到begin和end最终相遇,此时将相遇点的内容与key交换即可。(选取最左边的值作为key)
- 重复上述操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| void fastSort(int *data, int left,int right)
{
int temp,t;
if(left > right)
{
return;
}
temp = data[left];
int i = left;
int j = right;
while(i != j)
{
while(data[j] >= temp && i<j)
{
j--;
}
while(data[i] <= temp && i<j)
{
i++;
}
if(i < j)
{
t = data[i];
data[i] = data[j];
data[j] = t;
}
}
data[left] = data[i];
data[i] = temp;
fastSort(data,left,i-1);
fastSort(data,i+1,right);
return ;
}
|